Motivation
Each set of real values has a largest and a smallest element. This is a simple fact. However, if our set is made from vectors, the question for its largest or smallest one is no longer simple to answer. So far, the best answer is given by the notion of a Pareto set. This notion is based on a relation between vectors of real elements (mathematically its a semi-ordering relation), the so-called Pareto dominance relation. Given two vectors
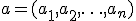 ,
,
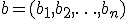
of same size, it is said that vector  Pareto dominates
Pareto dominates 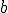 , if each component of
, if each component of  is smaller than or equal to the corresponding component of
is smaller than or equal to the corresponding component of 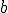 , and at least one component is smaller:
, and at least one component is smaller:
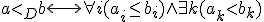
Thus, for example, the vector (1, 2, 6, 3) is Pareto dominating the vector (3, 3, 8, 5). Note that here, we are considering the minimum case only. Obviously, there is a corresponding definition for the maximum case as well, just by replacing the '<'-signs by '>'-signs.
For real numbers, or starting points, always either a ≤ b or b ≤ a is true. That will not hold for our just introduced Pareto dominance relation: for example, in the case of having the two vectors (2,12) and (4,8), the first one is not dominating the second one (its second element is larger), but the second one is also not dominating the first one (its first element is larger). A moment of reasoning gives that within a set of vectors, there will be pairs of vectors where one vector is dominating the other, and there will be other pairs of vectors, where none of them is dominating the other.
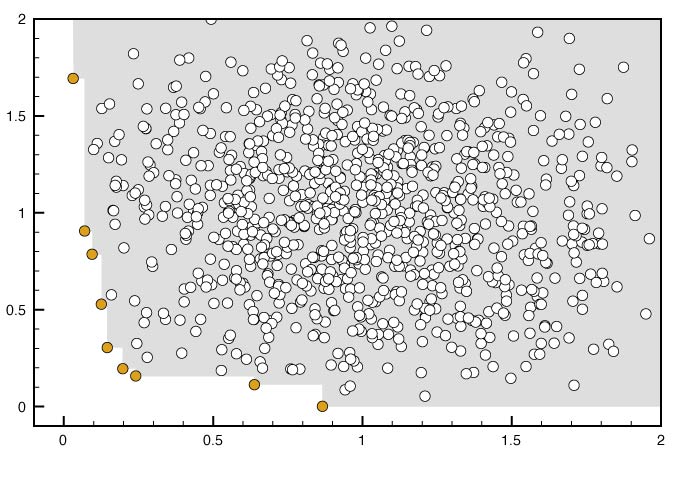
Fig. 1: The Pareto set of a set of points is the subset of all points, which are not dominated by any other point of the set.
A special group of vectors will not be dominated by any other vector of the set. In fig. 1, you can see around 1000 points, representing two-dimensional vectors by their coordinates. The points marked in orange do have this property: no other of the points of the set is dominating these points. Moreover, each of the remaining points is dominated by at least one of the orange points. They grey area indicates the region "monitored" by the orange points. Each additional point that is not located in the grey area is also not dominated by any of the points (orange ones, and white ones).
The orange points comprise the Pareto set of the set of all points. In general, its the subset of a set of vectors that is not dominated by any other vector of the set. The main difference to the "traditional" minimum of a set of real values is that there is usually more than one element of a set belonging to the Pareto set, means there is more than one "vector-minimum."
There is one drawback of the idea of the Pareto set: with increasing dimension of the vectors, the Pareto dominance relation becomes more and more unlikely. Consider an arbitrary vector with say 30 elements. For an other vector dominating this vector, all of its elements have to be smaller than the elements of the given vector. It can be easily understood that such a coincidence becomes more and more unlikely, as the number of elements of the vector increases. The expected number of dominated vectors of a set of m randomly choosen vectors in the n-dimensional unit cube (i.e. all elements are random numbers between 0 and 1) can be computed by the following formula:
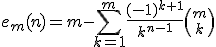
Play around with the following "rubylet" to see how rapidly these expectation values decrease with increasing vector dimension. Like in the figure above, for 1000 two-dimensional vectors we can expect about 992 dominated points. The Pareto set of the above example contains 9 points, so the expectation to have a dominated point seems rather high. However, for 1000 15-dimensional vectors, the average number of dominated vectors drops to 20, and for dimension 20, it is already below one. Nearly all points belong to the Pareto set, and it is no longer a useful means for distinguishing between the vectors.
The input fields in the rubylet refer to terms of evolutionary multi-objective optimization (EMO). Here, the dimension of the vectors equals the number of objectives of a multi-objective optimization problem. Its the n in the expression above. The number m of points is the size of the population. Many EMO algorithms directly employ the presence of Pareto dominance cases among the individuals of a population (i.e dominance among their fitness objectives), especially for reformulating the selection operator. So, in the MOGA algorithm [1], the probability of an individual to be selected (for mating) decreases with the number of individuals, by which it is dominated. In the famous NSGA-II algorithm [2], ranks are assigned to the individuals: rank 0 to all non-dominated individuals, rank 1 to all non-dominated individuals if neglecting all rank 0 individuals a.s.o. Individuals of smaller rank are more likely to be selected. These are just two examples for demonstrating, how directly such algorithms depend on the existence of dominated individuals at all. Having no dominance cases, these algorithms cannot work anymore.
Our research focussed on the question, how the Pareto concept can be made sustainable for larger number of objectives. The basic idea is to introduce degrees of Pareto dominance. The result, the so-called Fuzzy Pareto Dominance (FPD), will be introduced in the following section.
References
[1] Fonseca C.M., and P. J. Fleming. 1993. Genetic algorithm for multiobjective optimization: formulation, discussion and generalization. Proceedings of the Fifth International Conference on Genetic Algorithms, S. Forrest, ed. Morgan Kaufmann, San Mateo, 416-423. California : Morgan Kaufmann.
[2] Deb K., A. Pratap, S. Agarwal and T. Meyariva. 2002. A
fast and elitist multiobjective genetic algorithm:
NSGA-II. IEEE Transactions on Evolutionary
Computation, vol. 6, 182-197.
< FPD.Crowding | FPD.FPD | FPD.Definition >